Needle Optimization

Needle Optimization steps are performed in many other algorithms (Gradual Evolution,  Sensitivity-Directed Refinement, Deep Search versions, Robust algorithms).

You need the needle optimization algorithm if:

• You do not have a good starting design and cannot apply Refinement algorithms.
• You do not know the number of layers.
• You design a multilayer from scratch.
• You solve a complicated design problem.

As design total thickness is a very important and conservative parameter, an estimation of the total design thickness is necessary. You can start with any starting design, also with a single layer of enough thickness.

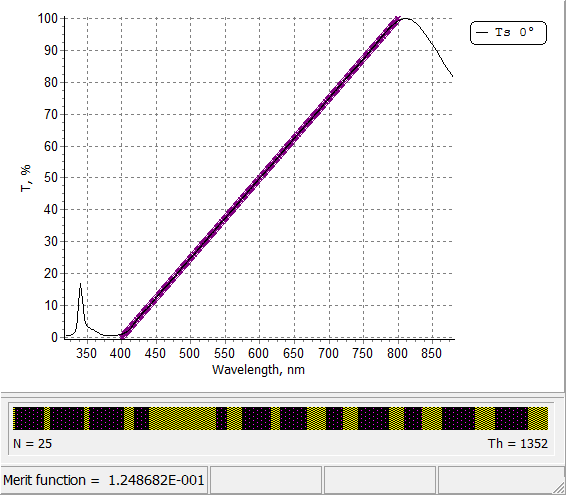
Fig. 1. Demonstration of designing a RAMP coating using needle optimization algorithm. Put the mouse on and out of the plot to see the animation.

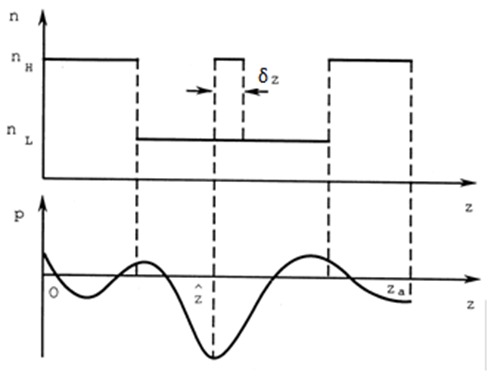
Fig. 2. Refractive index profile, \(P\)-function and needle variation.

Needle optimization algorithm introduces into consideration some new physical effects in multilayers by insertion new design layers, which are equivalent to variations of the refractive index profile (Fig. 2).

These variations are referred to as needle variations.

If new layers are inserted in proper places, then new interference effects associated with these layers improve the correspondence between actual and target spectral characteristics.

OptiLayer calculates the proper places automatically and then optimizes the layer thicknesses in the most effective way.

Due to some reasons, it may be required to define such places manually. This can be done through Needle Optimization (manual mode).

\[\delta MF=P(n_k,z)\cdot\delta z+o(\delta z) \qquad\;    (1)\]

An appropriate place for a needle variation corresponds to \(z-\) point where \(P\)-function takes its most negative value.

General schematic of the needle optimization algorithm is shown in Fig. 3.

When the number of coating materials exceeds two, an optimal material is chosen among all materials automatically in the most optimal way.

At the Refinement step, the same optimization methods are used (Fig. 4).

Unparalleled computation capability and outstanding efficiency of the Needle Optimization algorithm is due to unique know-how of OptiLayer.

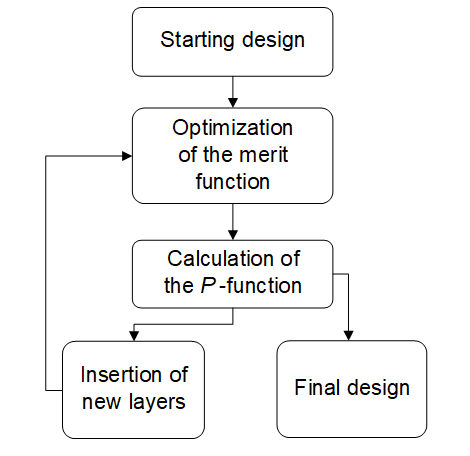
Fig. 3. Schematic of the needle optimization algorithm.

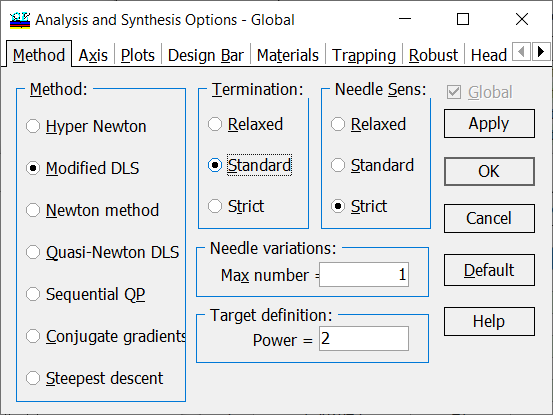
Fig. 4. Settings of parameters of optimization algorithms.

Synthesis –> Options –> Method tab

These settings allows you to choose:

• Optimization method at the Refinement step
• Termination criteria
• Needle sensitivity (for complicated problems Strict is recommended, for non-complicated problems Standard or relaxed)
• Number of needle variations in one iteration, power in the merit function (2 is a default value, the most typical one, recommended).

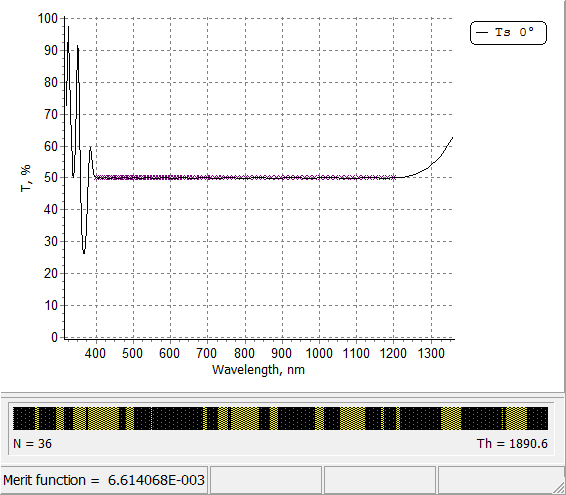
Fig. 5. Design of a broadband bemsplitter (put the mouse on and out of the picture)

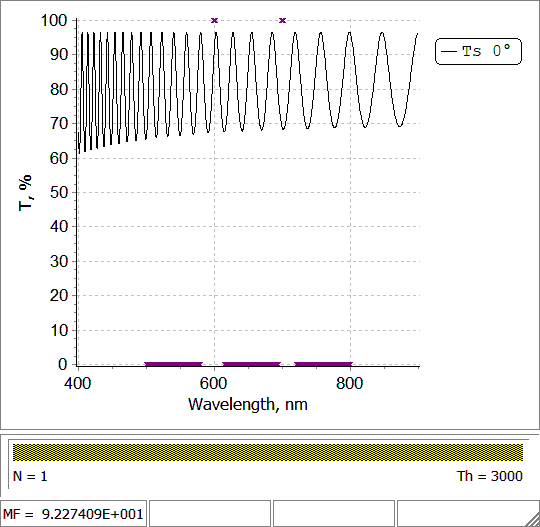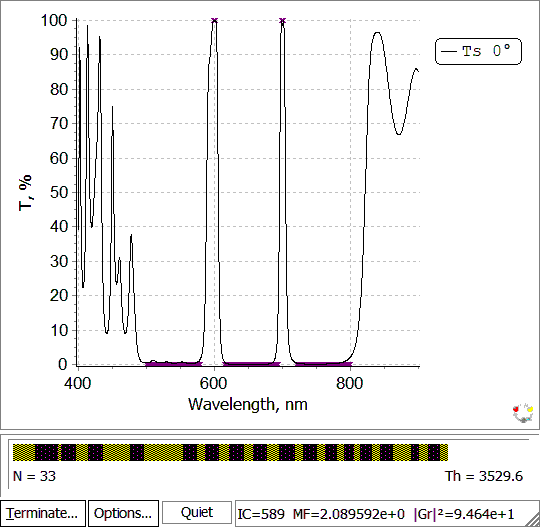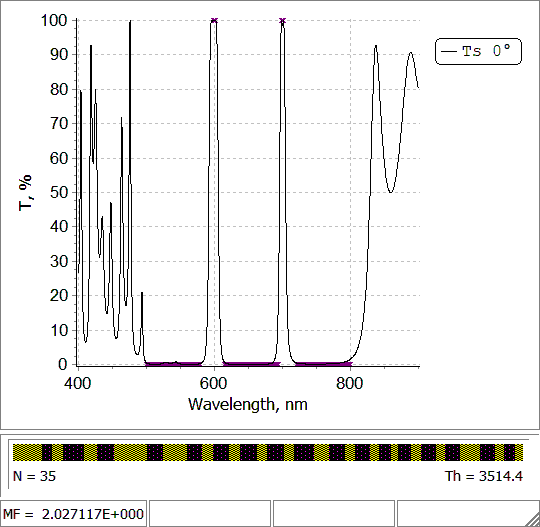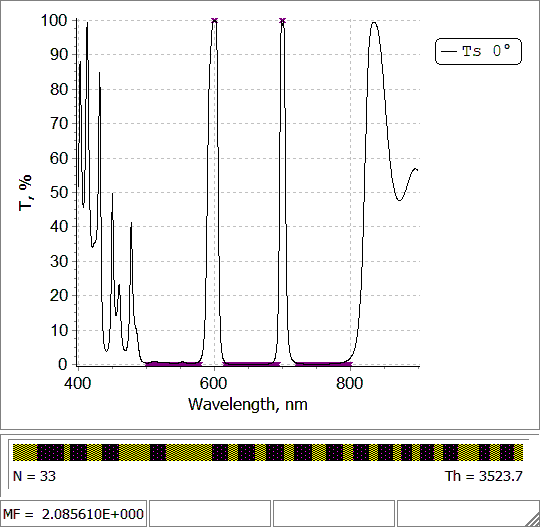
Fig. 6. Design of a two-line filter (put the mouse on and out of the picture)

See also our videos at YourTube :

• Designing broadband AR coatings

1. Sh. Furman and A.V.Tikhonravov, “Basics of optics of multilayer systems”, Editions Frontiers, Gif-sur Yvette, 1992, 242 p. This book can be free downloaded here.
2. A. V. Tikhonravov, M. K. Trubetskov, and G. W. DeBell, “Optical coating design approaches based on the needle optimization technique,” Appl. Opt. 46, 704-710 (2007).
3. A. V. Tikhonravov and M. K. Trubetskov, “Modern status and prospects of the development of methods of designing multilayer optical coatings,” J. Opt. Technol. 74, 845-850 (2007).
4. A. Tikhonravov and M. Trubetskov, “Modern design tools and a new paradigm in optical coating design,” Appl. Opt. 51, 7319-7332 (2012).
5. A. V. Tikhonravov, M. K. Trubetskov, and G. W. DeBell, “Application of the needle optimization technique to the design of optical coatings,” Appl. Opt. 35, 5493-5508 (1996).