Error analysis in stacks

Disturbed designs are calculated in the similar way as in the case of statistical errors analysis of conventional coatings.

Error analysis and Error Yield Analysis are powerful OptiLayer tools to study stability of design solutions to inevitable deposition errors.

Due to its high computational power, OptiLayer allows you to perform many hundreds and thousand statistical tests very fast.

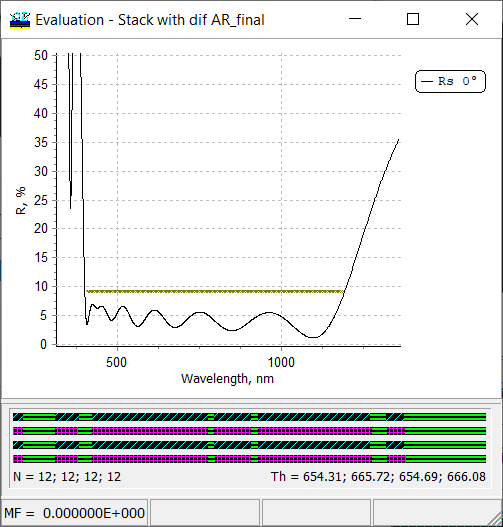
Fig. 1. Spectral characteristic of a stack containing four AR coatings. The stack operates in the range from 400 to 1200 nm. Error bars on the bottom panel represent designs in the stack. Thin-film materials are Nb₂O₅, TiO₂, and SiO₂. 

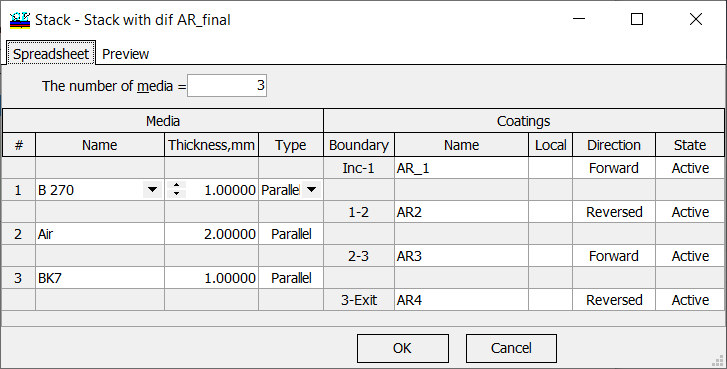
Fig. 2. Example. A stack consists of two substrates (B270 and BK7) separated by an air gap. Each surface is coated by AR coatings.

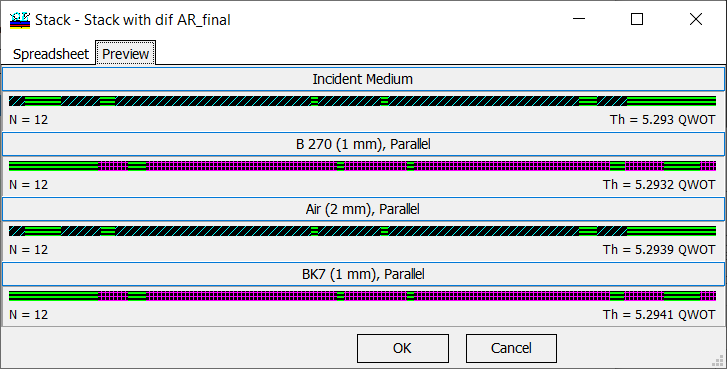
Fig. 3. The stack from Fig. 2 represented AR coatings in a graphical form.

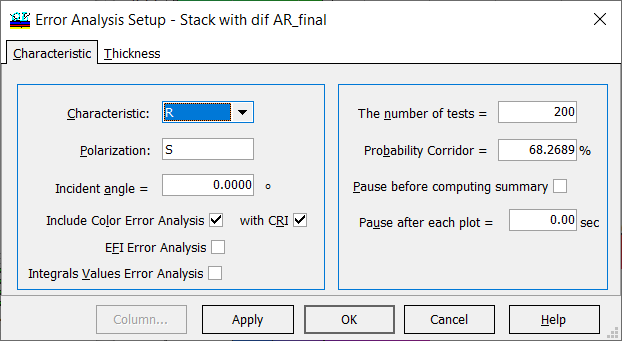
Fig. 4. Settings for error analysis in stacks. Color Error Analysis and CRI are also involved.

Levels of thickness errors are specified on the Thickness tab.

In Coating sub-tab (Fig. 5), it is possible to specify absolute or relative errors in all layers of each coatings of the stack.

In Materials sub-tab (Fig. 6), you can specify errors in layers of thin-film materials. Error Analysis and Color Error Analysis are shown in Figs. 8, 9, 10, and 11.

In Thickness sub-tab (Fig. 7), a fine tuning of deposition errors through the entire stack can be set up.

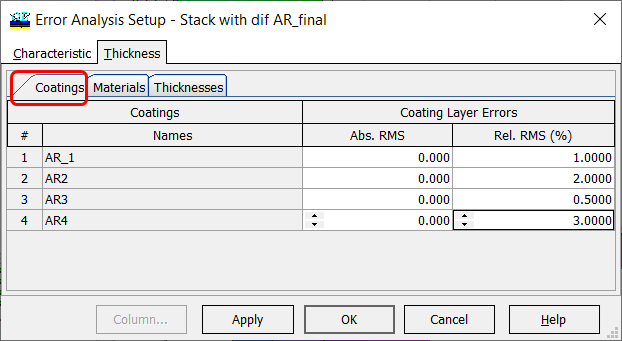
Fig. 5. Settings of errors in AR coatings. Level of relative errors are 1%, 2%, 0.5%, and 3%.

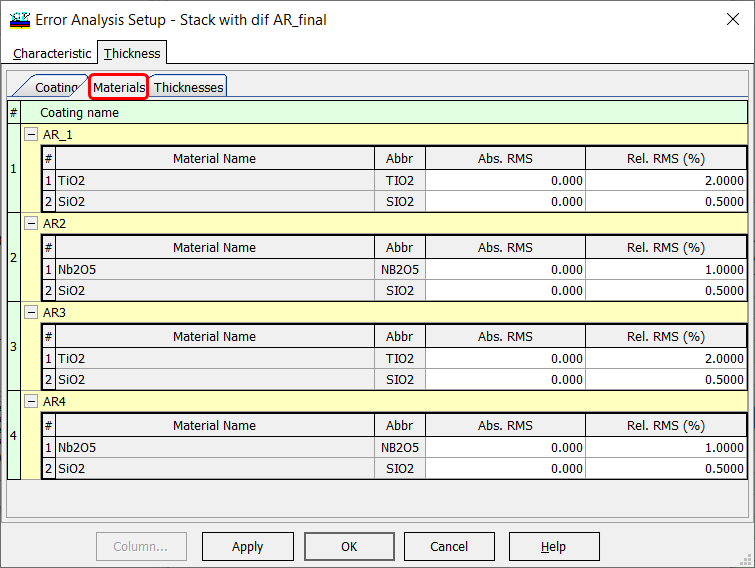
Fig. 6. Relative errors of 2%, 0.5%, and 1% are specified in TiO₂, SiO₂, and Nb₂O₅ layers.

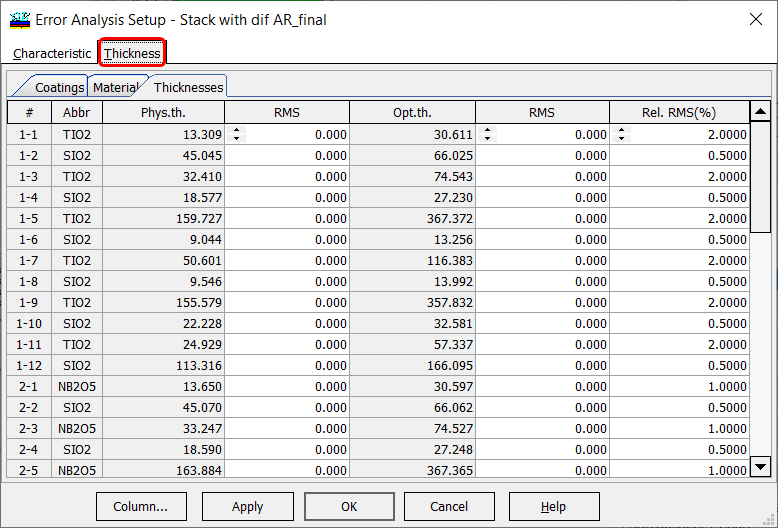
Fig. 7. Relative errors of 2%, 0.5%, and 1% are specified in TiO₂, SiO₂, and Nb₂O₅ layers. Using this Thickness sub-tab, you can specify error in each layer separately. This option is typically used for fine turning of expected errors.

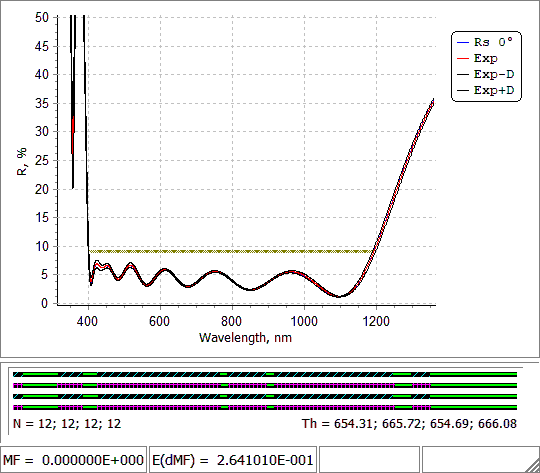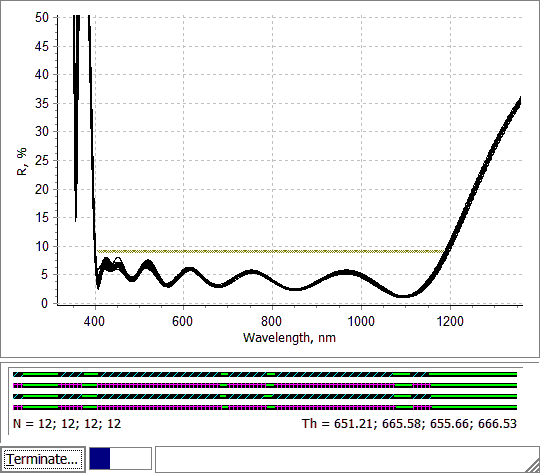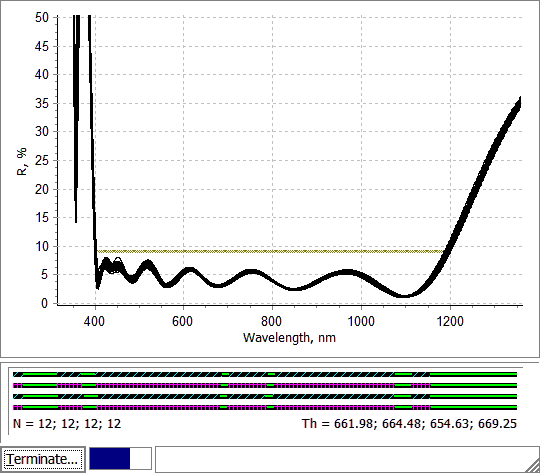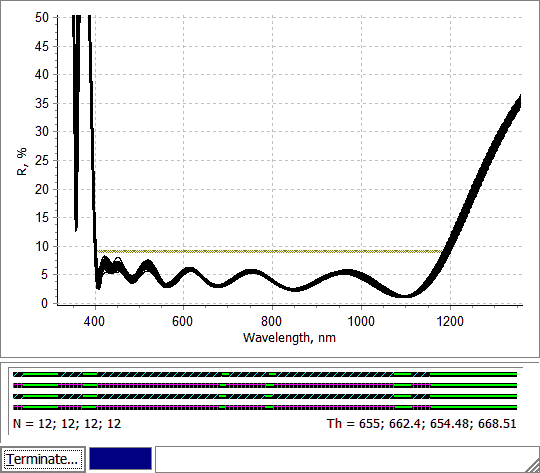
Fig. 8. Error analysis process for settings shown in Fig. 6.

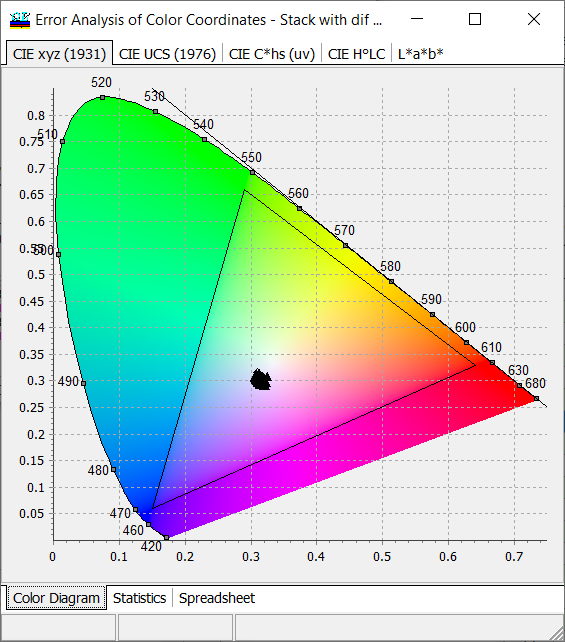
Fig. 9. Error analysis process for settings shown in Fig. 6. Error analysis of colors can be performed independently, i.e. it does not matter, whether a color target is specified. 

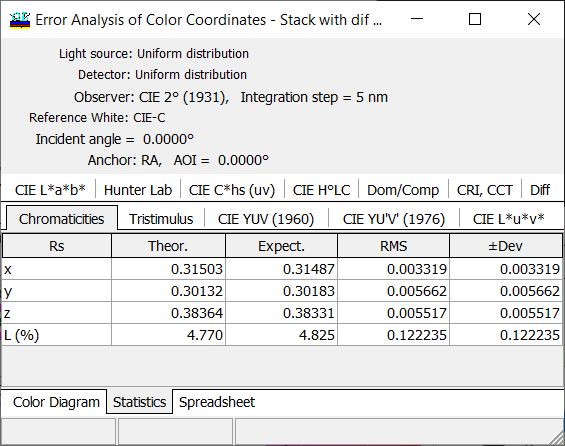
Fig. 10. Numerical values of the color deviations are presented in Statistics tab of the Error Analysis of Color Coordinates. Expect. denotes the average value of the color coordinates of disturbed designs and RMS and (\(\pm\) Dev) show root square deviation and deviations calculated for the specified value of Probability Corridor, respectively (Fig. 4). 

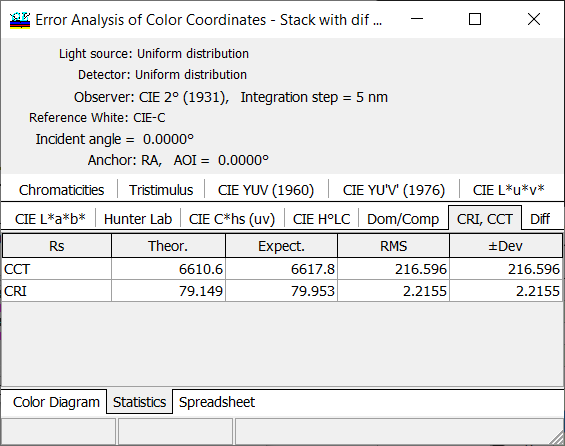
Fig. 11. Numerical values of CRI deviations are presented in Statistics tab of the Error Analysis of Color Coordinates. Expect. denotes the average value of CRI of disturbed designs and RMS and (\(\pm\) Dev) show root square deviation and deviations calculated for the specified value of Probability Corridor, respectively (Fig. 4). 

OptiLayer calculates statistical expectations and deviations of all values specified in Integrals, Values window. It does not matter whether these values in integral target indicated.

The Error Analysis of Integral, Values window has the same fonts, colors as Integral, Values window. Starting from the most recent version 12.83, you can define your own formatting style and restore it in all other problem directories.

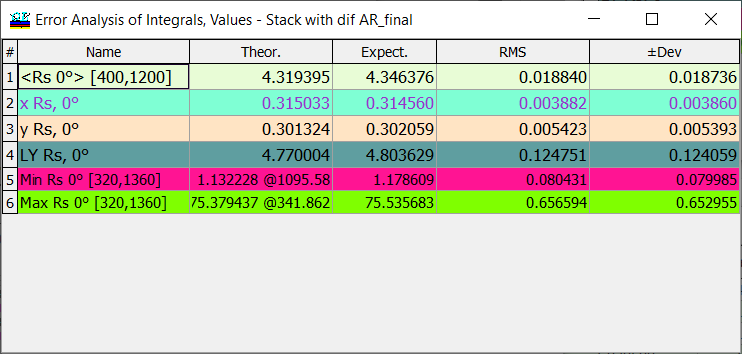
Fig. 12. Numerical values of deviations Integral values presented in Error Analysis of Integrals, Values. Expect. denotes the average value of the color coordinates of disturbed designs and RMS and (\(\pm\) Dev) show root square deviation and deviations calculated for the specified value of Probability Corridor, respectively. 

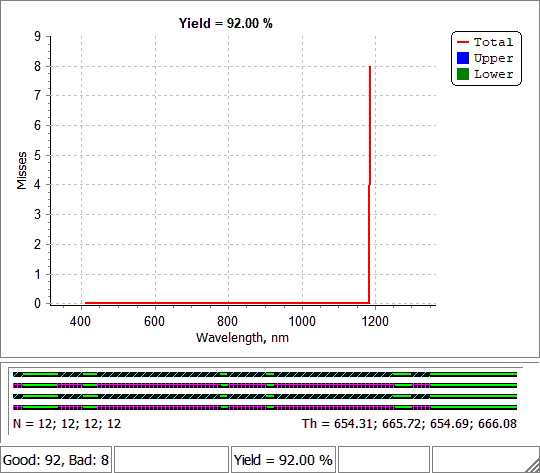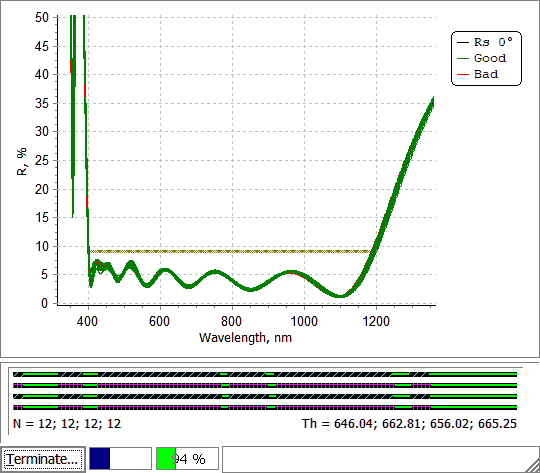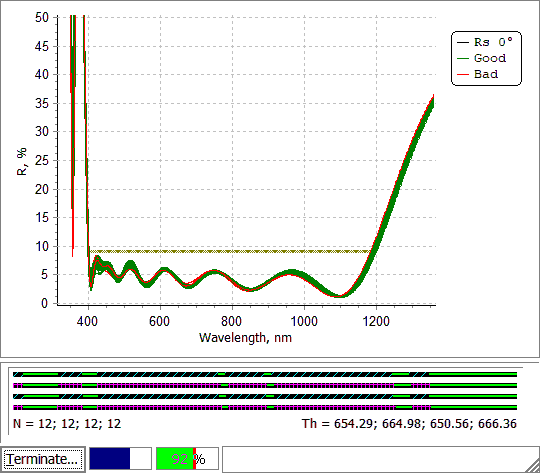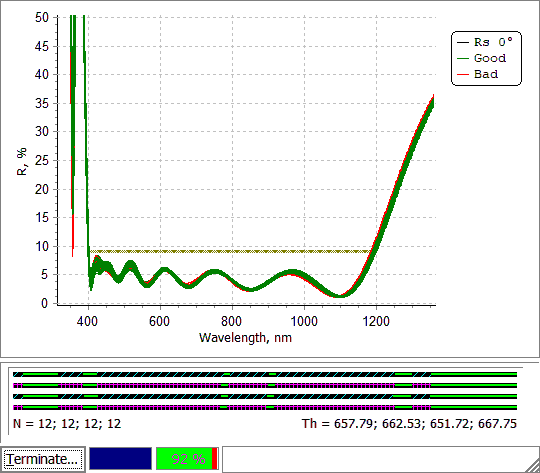
Fig. 13. Error Yield Analysis of the stack (Figs. 1 and 2) with settings shown in Figs. 6 and 7.

Yield bar on the bottom of the yield analysis window shows the current yield value. The number of statistical tests should be not very large in order not to slow down the calculations and not low in order to have a representative set of disturbed designs.

More details can be found here.

At the same time, yield estimations are performed only for AOI/polarization specified in the loaded range target.

Example in Fig.14: range target is specified for normal incidence, reflectance curves for 30 and 45 degrees, averaged polarization are shown as well.

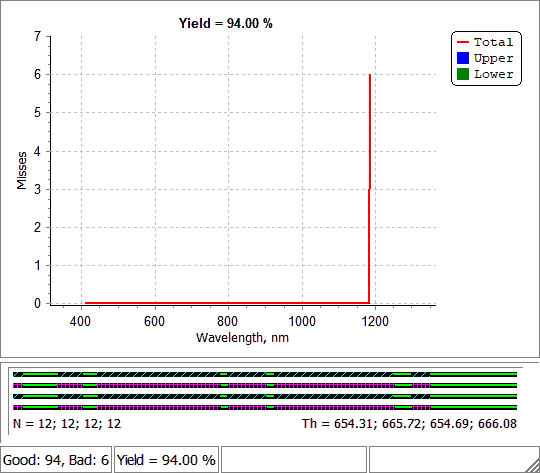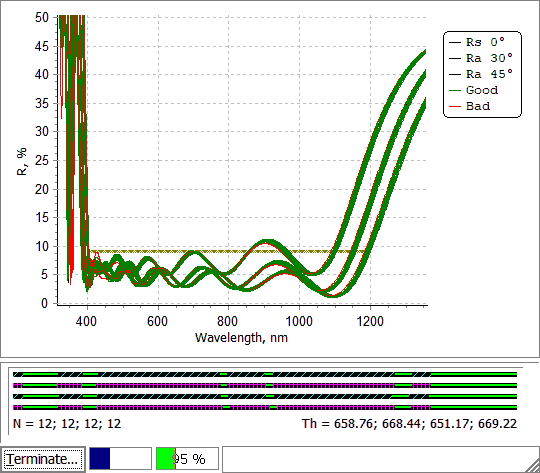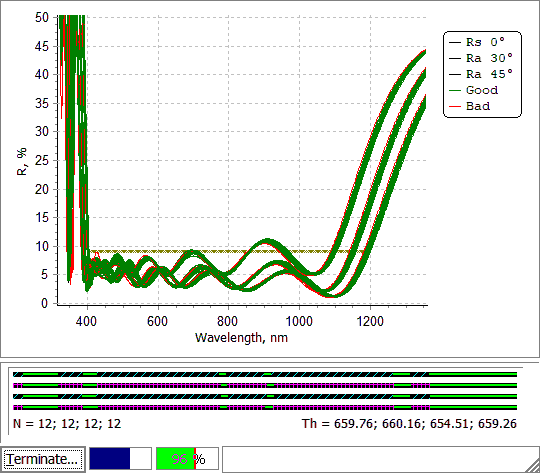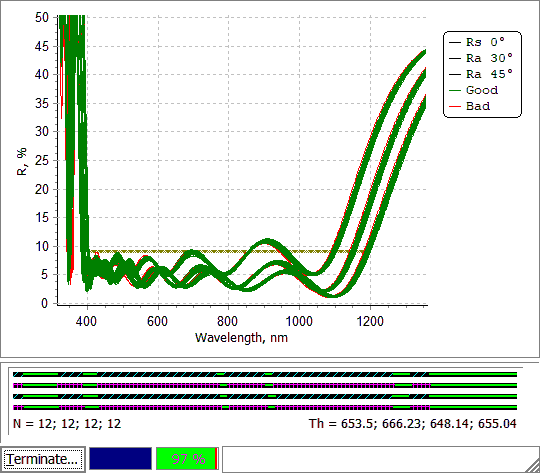
Fig. 14.  Error Yield Analysis of the stack (Figs. 1 and 2) with settings shown in Figs. 6 and 7. Yield is calculated for normal incidence, other two curves provide an impression of behavior of the disturbed spectral curves at oblique incidence.