| Random Errors mode performs a search for random errors in layer thickness. This search is a multiparametric inverse problem which solution may be unstable and non-unique.
One of the ways to overcome the ambiguity of the reverse engineering results is to involve more input experimental data, for example, multi-scan measurements. Random errors model assumes that different errors in coating layers. In this case the model coating is described by the vector \(X\): \[ X=(d_1+\delta_1,…,d_m+\delta_m), \] where \(d_1,…,d_m\) thicknesses of design layers, \(\delta_1,…,\delta_m\) absolute errors in layer thicknesses.
|
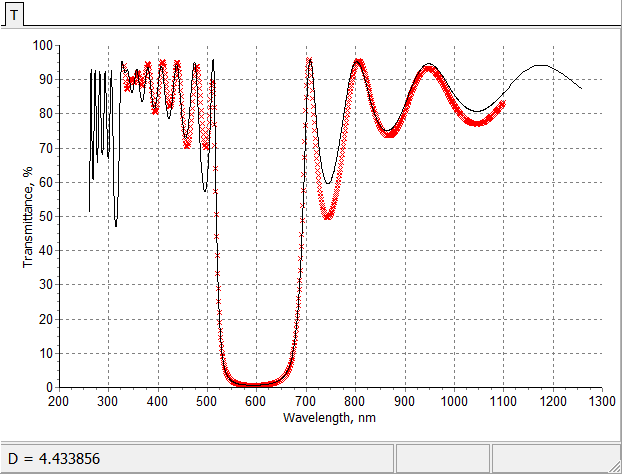 Initial fitting and final fitting after application of random errors model (put the mouse on and out of the picture). |
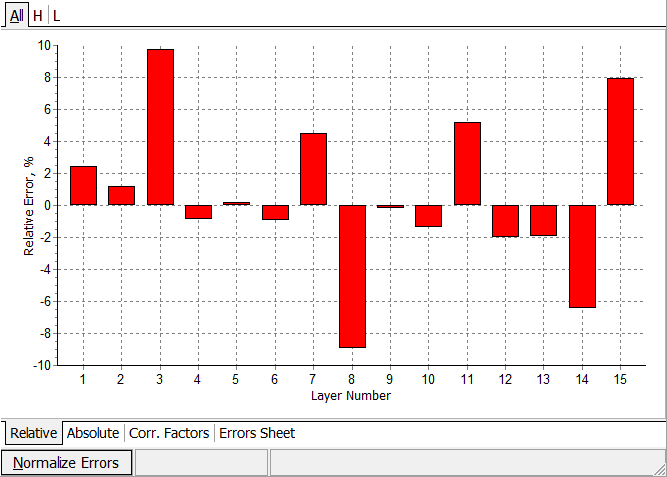
| Random errors algorithm is base on the minimization of the discrepancy function with respect to errors in layer thicknesses:
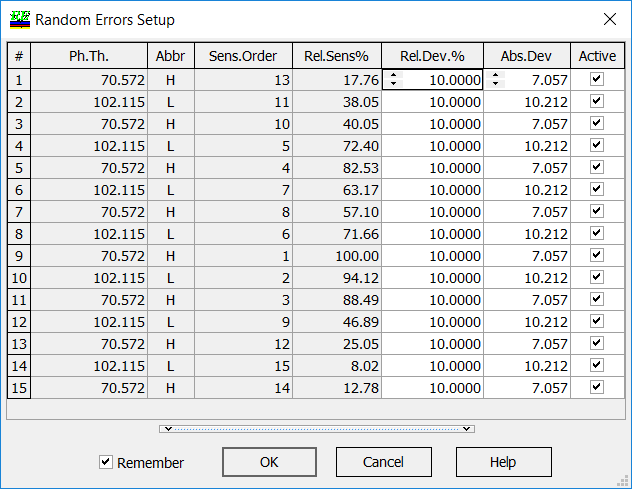
\[ DF=DF(\delta_1,…,\delta_m)\rightarrow \min \] In Random Errors Setup you can specify the upper boundaries of the errors. You can also specify what errors you are searching for (Active column).
|
 |
 |
The mathematical algorithms of OptiRE help you to overcome the problems connected with the instability and non-uniqueness of reverse engineering solutions.
Reverse engineering methodology is carefully studied in our publications. |
Application of this option is demonstrated and discussed in our publications:
|
|
OptiLayer provides user-friendly interface and a variety of examples allowing even a beginner to effectively start to design and characterize optical coatings. Read more…
Comprehensive manual in PDF format and e-mail support help you at each step of your work with OptiLayer.
If you are already an experienced user, OptiLayer gives your almost unlimited opportunities in solving all problems arising in design-production chain. Visit our publications page.
Look our video examples at YouTube
OptiLayer videos are available here:
Overview of Design/Analysis options of OptiLayer and overview of Characterization/Reverse Engineering options.
The videos were presented at the joint Agilent/OptiLayer webinar.