|
Most of the modern ultrafast laser systems include dispersive mirrors and other special coatings used for accurate phase control required for efficient pulse compression. Laser related coatings are multilayers providing specified group delay (GD) or/and group delay dispersion (GDD) as well as required spectral characteristic (for example, high reflectance). Specific features/requirements of these multilayers:
|
Design and production of these coatings require using effective numerical design algorithms and high precision deposition techniques.
OptiLayer provides all design tools for successful designing of complicated laser related coatings.
|
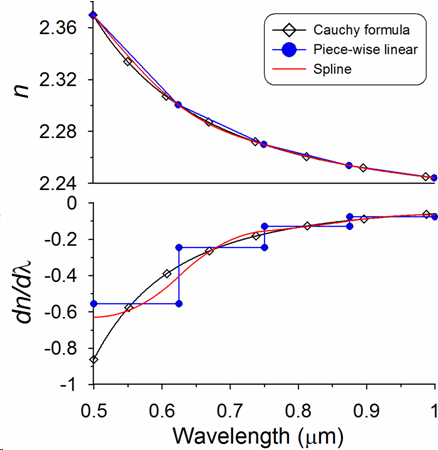
OptiLayer calculates all derivatives analytically! OptiLayer is only one software that provides such opportunity. Completely analytical approach + needle optimization technique allow to solve many challenging design problems in the field of laser related coatings. |
Main types of laser related coatings are:
|
One-octave Dispersive Mirror
|
 |
 |
“Classical approach” (Gradual evolution with combination of thin Layer Removal) leads to oscillations in GDD.
It is mathematically proved that oscillations of GDD are inevitable. It means that it is required to find a way to suppress them or to reduce their effect on the output pulse characteristics. OptiLayer provides various tricks/design tools to solve this problem. |
| Approach 1: Phase optimization with floating constants: Any given dependence \(GDD(\omega)\) can be integrated twice and converted to phase target:\[ \varphi(\omega)=\int\limits_{\omega_0}^\omega\int\limits_{\omega_0}^{\omega_1}GDD(\omega_2)d\omega_2+C_1\omega+C_2 \]\(C_1\) and \(C_2\) – arbitrary constants. Merit function now depends on these constants: \[ MF=F(d_1,…,d_m; C_1, C_2)\] |
For any set of thicknesses \(\{d_1,…,d_m\}\) constants can be excluded from the merit function analytically, because \(F\) is quadratic function with respect to \(C_1\) and \(C_2\):
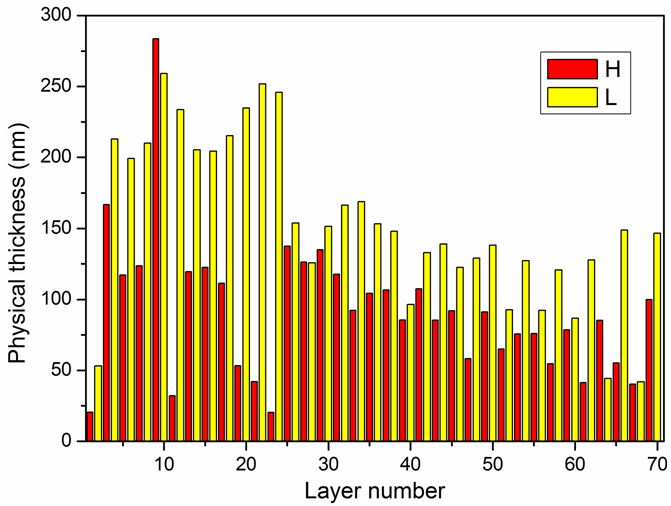
\[ \frac{\partial F}{\partial C_1}=0, \;\;\frac{\partial F}{\partial C_2}=0\] Resulting merit function is optimized with needle optimization technique. This approach can be applied to coatings of all types. Learn more… Result: 69-layer one-octave dispersive mirror. |
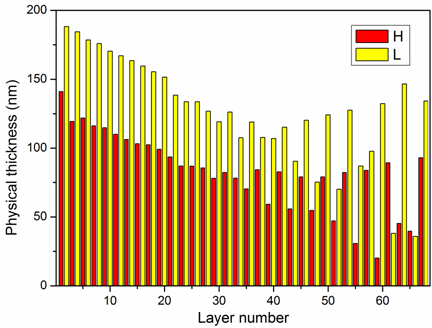 |
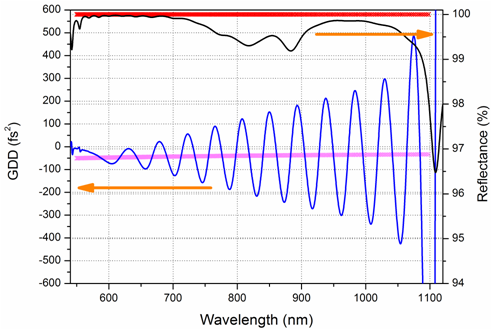
|
| Approach 2: Complimentary pairs
For dispersive mirror pair reflectance and GDD can be defined as: \[ R_p=\sqrt{R_1\cdot R_2}; \;\; GDD_p=\frac{GDD_1+GDD_2}{2} \]
|
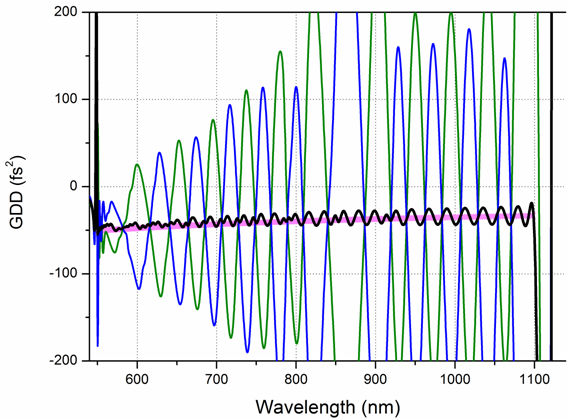
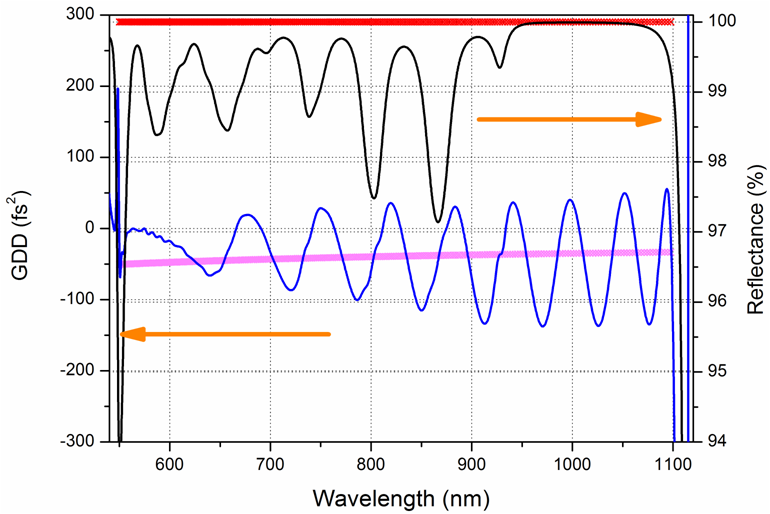
Result: A pair of 72-layer and 70-layer dispersive mirrors (complimentary pair). Green and blue curves represent GDD of two diespersive mirrors and black curve shows resulting GDD |
Application of robust algorithm to designing dispersive mirrors
| OptiLayer allows taking into account requirement on stability of the design on errors in layer parameters. This requirement is very important for ultrafast coatings.
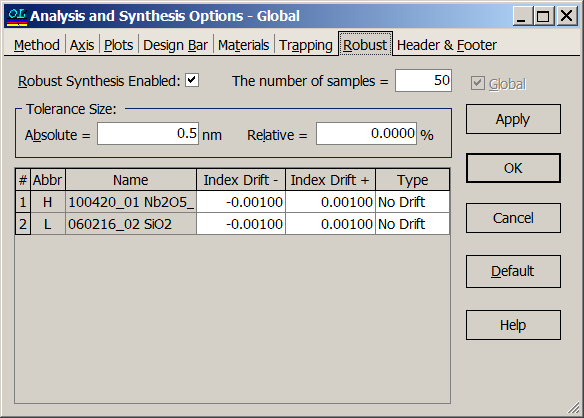
Example: Dispersive mirror that has to compensate GDD of -200 fs2 in the spectral range from 700 to 900 nm. Substrate: B260 glass; Layer Materials: Nb2O5 and SiO2. |
All OptiLayer algorithms can work in the Robust mode. Absolute errors in layer thicknesses can be estimated at the \(\sigma=0.5\) nm level:
|
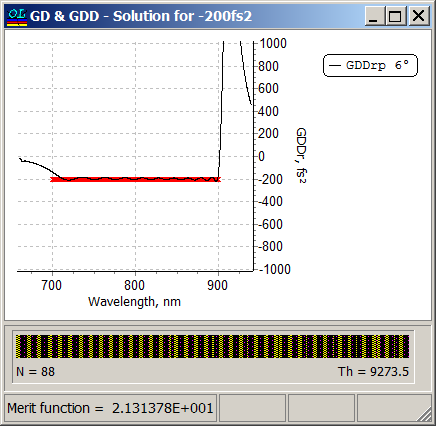
| Convenient design solution: 88 layers, total thickness 9273.5 nm. Excellent GDD spectral performance has been obtained:
|
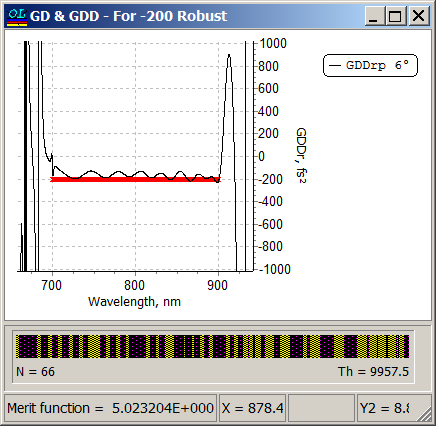
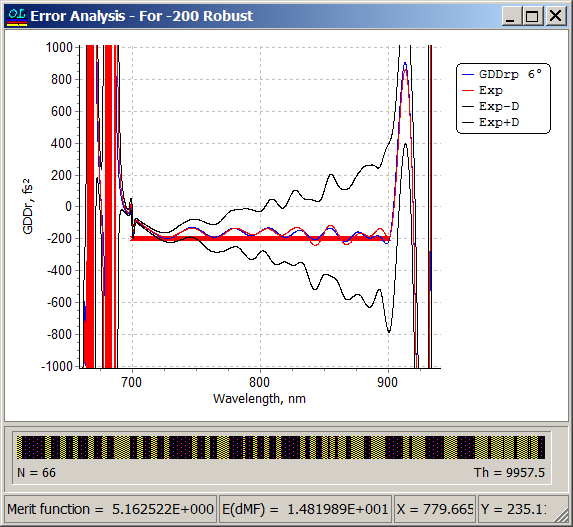
Robust design solution: 66 layers, total thickness 9957.5 nm. Good GDD spectral performance has been achieved:
|
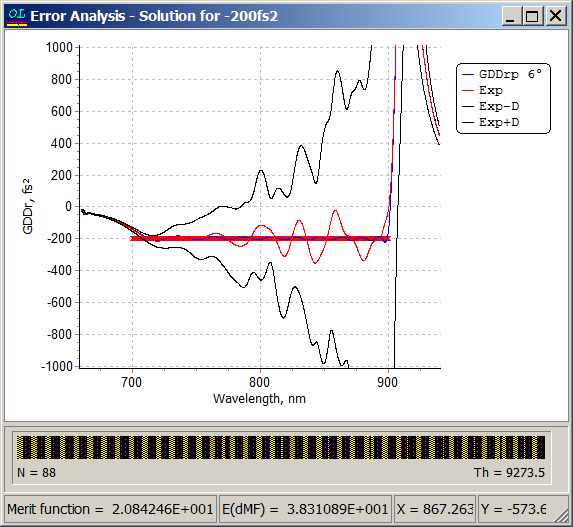
| Error analysis of the convenient design solution: level of absolute thickness errors of 0.5 nm was specified.
|
Error analysis of the robust design solution at the same level of absolute thickness errors. It is obvious, that the design is more stable.
|
Learn more in our publications:
|
|